背景引入
这里第一次接触过 线上慎用 BigDecimal ,坑的差点被开了
《阿里巴巴 Java 开发手册》中提到:“为了避免精度丢失,可以使用 BigDecimal 来进行浮点数的运算”。
下面是实践:
Float a = 2.0 f - 1.9 f;
Float b = 1.8 f - 1.7 f;
System.Out.Println (a);// 0.100000024
System.Out.Println (b);// 0.099999905
System.Out.Println (a == b);// false
为什么浮点数 float 或 double 运算的时候会有精度丢失的风险呢?
这个和计算机保存浮点数的机制有很大关系。我们知道计算机是二进制的,而且计算机在表示一个数字时,宽度是有限的,无限循环的小数存储在计算机时,只能被截断,所以就会导致小数精度发生损失的情况。这也就是解释了为什么浮点数没有办法用二进制精确表示。
就比如说十进制下的 0.2 就没办法精确转换成二进制小数:
// 0.2 转换为二进制数的过程为,不断乘以 2,直到不存在小数为止,
// 在这个计算过程中,得到的整数部分从上到下排列就是二进制的结果。
0.2 * 2 = 0.4 -> 0
0.4 * 2 = 0.8 -> 0
0.8 * 2 = 1.6 -> 1
0.6 * 2 = 1.2 -> 1
0.2 * 2 = 0.4 -> 0(发生循环)
...我搜藏了一篇文章,关于浮点数运算的:组成原理(三)下——浮点数运算
BigDecimal 介绍
BigDecimal 可以实现对浮点数的运算,不会造成精度丢失。
通常情况下,大部分需要浮点数精确运算结果的业务场景(比如涉及到钱的场景)都是通过 BigDecimal 来做的。
《阿里巴巴 Java 开发手册》中提到:浮点数之间的等值判断,基本数据类型不能用 == 来比较,包装数据类型不能用 equals 来判断。
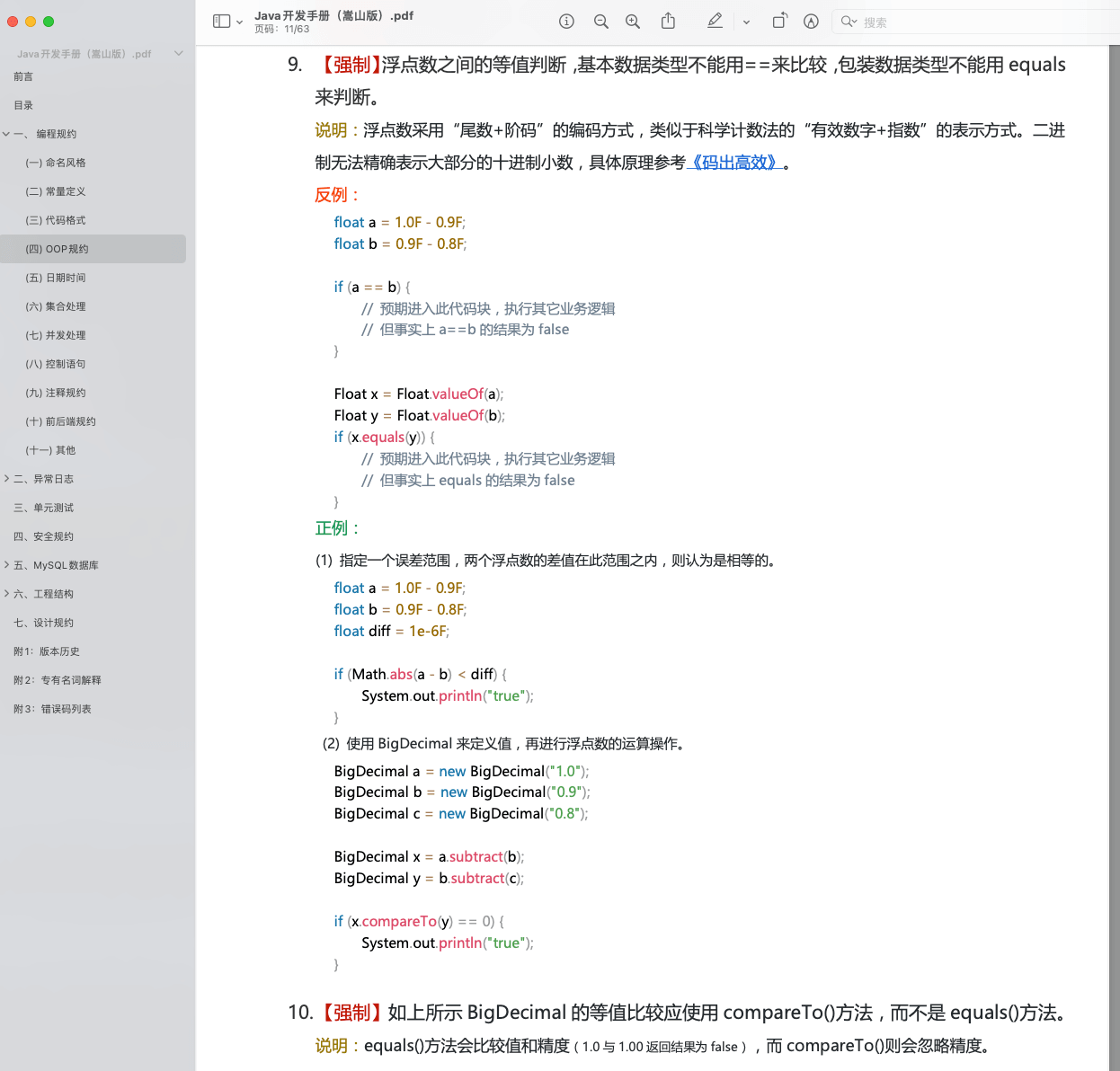
具体原因我们在上面已经详细介绍了,这里就不多提了。
想要解决浮点数运算精度丢失这个问题,可以直接使用 BigDecimal 来定义浮点数的值,然后再进行浮点数的运算操作即可。
BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("0.9");
BigDecimal c = new BigDecimal("0.8");
BigDecimal x = a.subtract(b);
BigDecimal y = b.subtract(c);
System.out.println(x.compareTo(y));// 0BigDecimal 常见方法
创建
我们在使用 BigDecimal 时,为了防止精度丢失,推荐使用它的 BigDecimal(String val) 构造方法或者 BigDecimal.valueOf(double val) 静态方法来创建对象。
《阿里巴巴 Java 开发手册》对这部分内容也有提到,如下图所示。

加减乘除
add 方法用于将两个 BigDecimal 对象相加,subtract 方法用于将两个 BigDecimal 对象相减。multiply 方法用于将两个 BigDecimal 对象相乘,divide 方法用于将两个 BigDecimal 对象相除。
BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("0.9");
System.out.println(a.add(b));// 1.9
System.out.println(a.subtract(b));// 0.1
System.out.println(a.multiply(b));// 0.90
System.out.println(a.divide(b));// 无法除尽,抛出 ArithmeticException 异常
System.out.println(a.divide(b, 2, RoundingMode.HALF_UP));// 1.11这里需要注意的是,在我们使用 divide 方法的时候尽量使用 3 个参数版本,并且 RoundingMode 不要选择 UNNECESSARY,否则很可能会遇到 ArithmeticException(无法除尽出现无限循环小数的时候),其中 scale 表示要保留几位小数,roundingMode 代表保留规则。
public BigDecimal divide(BigDecimal divisor, int scale, RoundingMode roundingMode) {
return divide(divisor, scale, roundingMode.oldMode);
}保留规则非常多,这里列举几种:
public enum RoundingMode {
// 2.5 -> 3 , 1.6 -> 2
// -1.6 -> -2 , -2.5 -> -3
UP(BigDecimal.ROUND_UP),
// 2.5 -> 2 , 1.6 -> 1
// -1.6 -> -1 , -2.5 -> -2
DOWN(BigDecimal.ROUND_DOWN),
// 2.5 -> 3 , 1.6 -> 2
// -1.6 -> -1 , -2.5 -> -2
CEILING(BigDecimal.ROUND_CEILING),
// 2.5 -> 2 , 1.6 -> 1
// -1.6 -> -2 , -2.5 -> -3
FLOOR(BigDecimal.ROUND_FLOOR),
// 2.5 -> 3 , 1.6 -> 2
// -1.6 -> -2 , -2.5 -> -3
HALF_UP(BigDecimal.ROUND_HALF_UP),
//......
}大小比较
a.compareTo(b) : 返回 -1 表示 a 小于 b,0 表示 a 等于 b , 1 表示 a 大于 b。
BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("0.9");
System.out.println(a.compareTo(b));// 1保留几位小数
通过 setScale 方法设置保留几位小数以及保留规则。保留规则有挺多种,不需要记,IDEA 会提示。
BigDecimal m = new BigDecimal("1.255433");
BigDecimal n = m.setScale(3,RoundingMode.HALF_DOWN);
System.out.println(n);// 1.255BigDecimal 等值比较问题
《阿里巴巴 Java 开发手册》中提到:

BigDecimal 使用 equals() 方法进行等值比较出现问题的代码示例:
BigDecimal a = new BigDecimal("1");
BigDecimal b = new BigDecimal("1.0");
System.out.println(a.equals(b));//false这是因为 equals() 方法不仅仅会比较值的大小(value)还会比较精度(scale),而 compareTo() 方法比较的时候会忽略精度。
1.0 的 scale 是 1,1 的 scale 是 0,因此 a.equals(b) 的结果是 false。

compareTo() 方法可以比较两个 BigDecimal 的值,如果相等就返回 0,如果第 1 个数比第 2 个数大则返回 1,反之返回-1。
BigDecimal a = new BigDecimal("1");
BigDecimal b = new BigDecimal("1.0");
System.out.println(a.compareTo(b));//0BigDecimal 工具类分享
网上有一个使用人数比较多的 BigDecimal 工具类,提供了多个静态方法来简化 BigDecimal 的操作。
我对其进行了简单改进,分享一下源码:
import java.math.BigDecimal;
import java.math.RoundingMode;
/**
* 简化BigDecimal计算的小工具类
*/
public class BigDecimalUtil {
/**
* 默认除法运算精度
*/
private static final int DEF_DIV_SCALE = 10;
private BigDecimalUtil() {
}
/**
* 提供精确的加法运算。
*
* @param v1 被加数
* @param v2 加数
* @return 两个参数的和
*/
public static double add(double v1, double v2) {
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.add(b2).doubleValue();
}
/**
* 提供精确的减法运算。
*
* @param v1 被减数
* @param v2 减数
* @return 两个参数的差
*/
public static double subtract(double v1, double v2) {
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.subtract(b2).doubleValue();
}
/**
* 提供精确的乘法运算。
*
* @param v1 被乘数
* @param v2 乘数
* @return 两个参数的积
*/
public static double multiply(double v1, double v2) {
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.multiply(b2).doubleValue();
}
/**
* 提供(相对)精确的除法运算,当发生除不尽的情况时,精确到
* 小数点以后10位,以后的数字四舍五入。
*
* @param v1 被除数
* @param v2 除数
* @return 两个参数的商
*/
public static double divide(double v1, double v2) {
return divide(v1, v2, DEF_DIV_SCALE);
}
/**
* 提供(相对)精确的除法运算。当发生除不尽的情况时,由scale参数指
* 定精度,以后的数字四舍五入。
*
* @param v1 被除数
* @param v2 除数
* @param scale 表示表示需要精确到小数点以后几位。
* @return 两个参数的商
*/
public static double divide(double v1, double v2, int scale) {
if (scale < 0) {
throw new IllegalArgumentException(
"The scale must be a positive integer or zero");
}
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.divide(b2, scale, RoundingMode.HALF_EVEN).doubleValue();
}
/**
* 提供精确的小数位四舍五入处理。
*
* @param v 需要四舍五入的数字
* @param scale 小数点后保留几位
* @return 四舍五入后的结果
*/
public static double round(double v, int scale) {
if (scale < 0) {
throw new IllegalArgumentException(
"The scale must be a positive integer or zero");
}
BigDecimal b = BigDecimal.valueOf(v);
BigDecimal one = new BigDecimal("1");
return b.divide(one, scale, RoundingMode.HALF_UP).doubleValue();
}
/**
* 提供精确的类型转换(Float)
*
* @param v 需要被转换的数字
* @return 返回转换结果
*/
public static float convertToFloat(double v) {
BigDecimal b = new BigDecimal(v);
return b.floatValue();
}
/**
* 提供精确的类型转换(Int)不进行四舍五入
*
* @param v 需要被转换的数字
* @return 返回转换结果
*/
public static int convertsToInt(double v) {
BigDecimal b = new BigDecimal(v);
return b.intValue();
}
/**
* 提供精确的类型转换(Long)
*
* @param v 需要被转换的数字
* @return 返回转换结果
*/
public static long convertsToLong(double v) {
BigDecimal b = new BigDecimal(v);
return b.longValue();
}
/**
* 返回两个数中大的一个值
*
* @param v1 需要被对比的第一个数
* @param v2 需要被对比的第二个数
* @return 返回两个数中大的一个值
*/
public static double returnMax(double v1, double v2) {
BigDecimal b1 = new BigDecimal(v1);
BigDecimal b2 = new BigDecimal(v2);
return b1.max(b2).doubleValue();
}
/**
* 返回两个数中小的一个值
*
* @param v1 需要被对比的第一个数
* @param v2 需要被对比的第二个数
* @return 返回两个数中小的一个值
*/
public static double returnMin(double v1, double v2) {
BigDecimal b1 = new BigDecimal(v1);
BigDecimal b2 = new BigDecimal(v2);
return b1.min(b2).doubleValue();
}
/**
* 精确对比两个数字
*
* @param v1 需要被对比的第一个数
* @param v2 需要被对比的第二个数
* @return 如果两个数一样则返回0,如果第一个数比第二个数大则返回1,反之返回-1
*/
public static int compareTo(double v1, double v2) {
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.compareTo(b2);
}
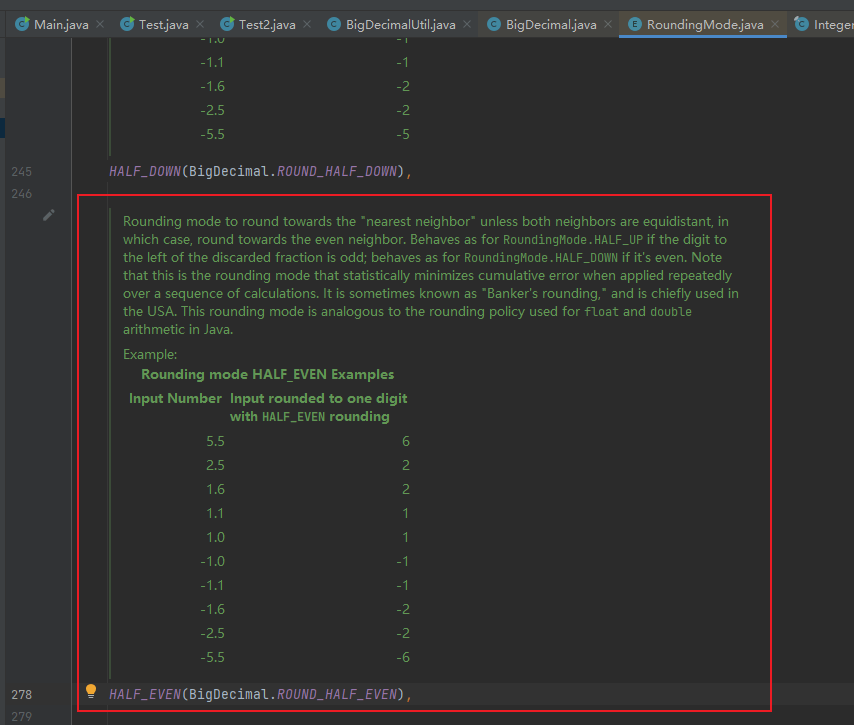
}相关 issue:建议对保留规则设置为 RoundingMode. HALF_EVEN, 即四舍六入五成双 。
总结
浮点数没有办法用二进制精确表示,因此存在精度丢失的风险。
不过,Java 提供了 BigDecimal 来操作浮点数。BigDecimal 的实现利用到了 BigInteger (用来操作大整数), 所不同的是 BigDecimal 加入了小数位的概念。