2. 二维矩阵中的前缀和

这是力扣第 304 题「二维区域和检索 - 矩阵不可变」，其实和上一题类似，上一题是让你计算子数组的元素之和，这道题让你计算二维矩阵中子矩阵的元素之和：

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

示例 1：

**输入:** 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
**输出:** 
[null, 8, 11, 12]

**解释:**
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
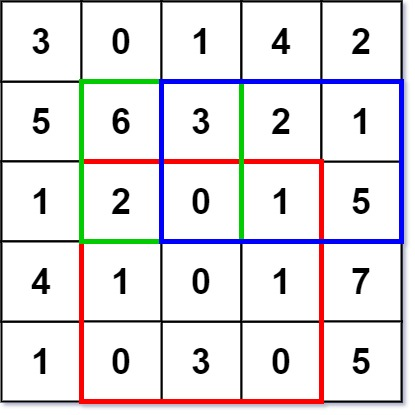
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -105 <= matrix[i][j] <= 105
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• 最多调用 104 次 sumRegion 方法

比如说输入的 matrix 如下图：

按照题目要求，矩阵左上角为坐标原点 (0, 0)，那么 sumRegion([2,1,4,3]) 就是图中红色的子矩阵，你需要返回该子矩阵的元素和 8。

当然，你可以用一个嵌套 for 循环去遍历这个矩阵，但这样的话 sumRegion 函数的时间复杂度就高了，你算法的格局就低了。

注意任意子矩阵的元素和可以转化成它周边几个大矩阵的元素和的运算：

而这四个大矩阵有一个共同的特点，就是左上角都是 (0, 0) 原点。

那么做这道题更好的思路和一维数组中的前缀和是非常类似的，我们可以维护一个二维 preSum 数组，专门记录以原点为顶点的矩阵的元素之和，就可以用几次加减运算算出任何一个子矩阵的元素和：

class NumMatrix {
    // 定义：preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和
    private int[][] preSum;
    
    public NumMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        if (m == 0 || n == 0) return;
        // 构造前缀和矩阵
        preSum = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                // 计算每个矩阵 [0, 0, i, j] 的元素和
                preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
            }
        }
    }
    
    // 计算子矩阵 [x1, y1, x2, y2] 的元素和
    public int sumRegion(int x1, int y1, int x2, int y2) {
        // 目标矩阵之和由四个相邻矩阵运算获得
        return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
    }
}

这样，sumRegion 函数的时间复杂度也用前缀和技巧优化到了 O(1)，这是典型的「空间换时间」思路。

前缀和技巧就讲到这里，应该说这个算法技巧是会者不难难者不会，实际运用中还是要多培养自己的思维灵活性，做到一眼看出题目是一个前缀和问题。