图是一种较为复杂的非线性结构。 为啥说其较为复杂呢?
根据前面的内容,我们知道:
- 线性数据结构的元素满足唯一的线性关系,每个元素(除第一个和最后一个外)只有一个直接前趋和一个直接后继。
- 树形数据结构的元素之间有着明显的层次关系。
但是,图形结构的元素之间的关系是任意的。
何为图呢? 简单来说,图就是由顶点的有穷非空集合和顶点之间的边组成的集合。通常表示为:G(V,E),其中,G 表示一个图,V 表示顶点的集合,E 表示边的集合。
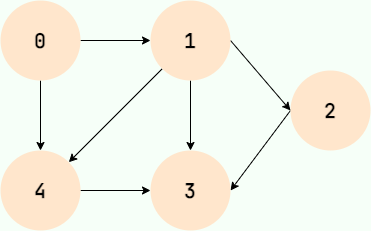
下图所展示的就是图这种数据结构,并且还是一张有向图。
图在我们日常生活中的例子很多!比如我们在社交软件上好友关系就可以用图来表示。
图的基本概念
顶点
图中的数据元素,我们称之为顶点,图至少有一个顶点(非空有穷集合)
对应到好友关系图,每一个用户就代表一个顶点。
边
顶点之间的关系用边表示。
对应到好友关系图,两个用户是好友的话,那两者之间就存在一条边。
度
度表示一个顶点包含多少条边,在有向图中,还分为出度和入度,出度表示从该顶点出去的边的条数,入度表示进入该顶点的边的条数。
对应到好友关系图,度就代表了某个人的好友数量。
无向图和有向图
边表示的是顶点之间的关系,有的关系是双向的,比如同学关系,A 是 B 的同学,那么 B 也肯定是 A 的同学,那么在表示 A 和 B 的关系时,就不用关注方向,用不带箭头的边表示,这样的图就是无向图。
有的关系是有方向的,比如父子关系,师生关系,微博的关注关系,A 是 B 的爸爸,但 B 肯定不是 A 的爸爸,A 关注 B,B 不一定关注 A。在这种情况下,我们就用带箭头的边表示二者的关系,这样的图就是有向图。
无权图和带权图
对于一个关系,如果我们只关心关系的有无,而不关心关系有多强,那么就可以用无权图表示二者的关系。
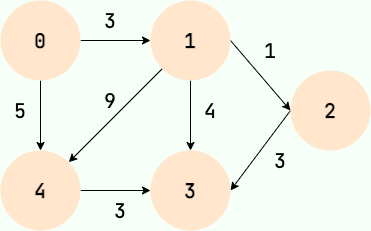
对于一个关系,如果我们既关心关系的有无,也关心关系的强度,比如描述地图上两个城市的关系,需要用到距离,那么就用带权图来表示,带权图中的每一条边一个数值表示权值,代表关系的强度。
下图就是一个带权有向图。
图的存储
邻接矩阵存储
邻接矩阵将图用二维矩阵存储,是一种较为直观的表示方式。
如果第 i 个顶点和第 j 个顶点之间有关系,且关系权值为 n,则 A[i][j]=n 。
在无向图中,我们只关心关系的有无,所以当顶点 i 和顶点 j 有关系时,A[i][j]=1,当顶点 i 和顶点 j 没有关系时,A[i][j]=0。如下图所示:
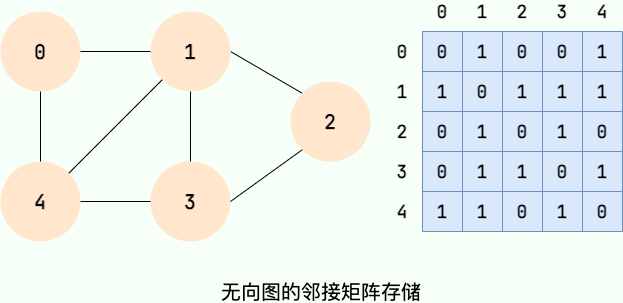
值得注意的是:无向图的邻接矩阵是一个对称矩阵,因为在无向图中,顶点 i 和顶点 j 有关系,则顶点 j 和顶点 i 必有关系。

邻接矩阵存储的方式优点是简单直接(直接使用一个二维数组即可),并且,在获取两个定点之间的关系的时候也非常高效(直接获取指定位置的数组元素的值即可)。但是,这种存储方式的缺点也比较明显,那就是比较浪费空间,
邻接表存储
针对上面邻接矩阵比较浪费内存空间的问题,诞生了图的另外一种存储方法—邻接表 。
邻接链表使用一个链表来存储某个顶点的所有后继相邻顶点。对于图中每个顶点 Vi,把所有邻接于 Vi 的顶点 Vj 链成一个单链表,这个单链表称为顶点 Vi 的 邻接表。如下图所示:
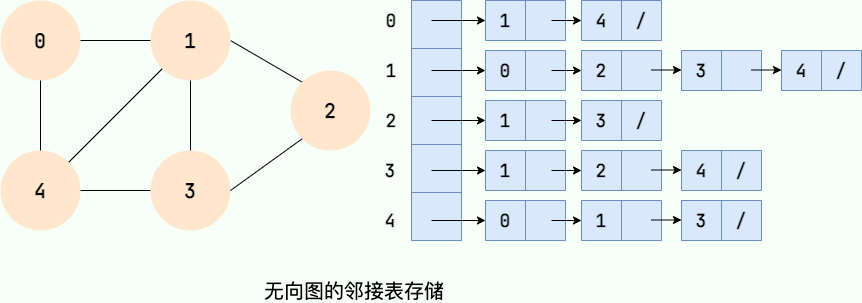

大家可以数一数邻接表中所存储的元素的个数以及图中边的条数,你会发现:
- 在无向图中,邻接表元素个数等于边的条数的两倍,如左图所示的无向图中,边的条数为 7,邻接表存储的元素个数为 14。
- 在有向图中,邻接表元素个数等于边的条数,如右图所示的有向图中,边的条数为 8,邻接表存储的元素个数为 8。
图的搜索
广度优先搜索
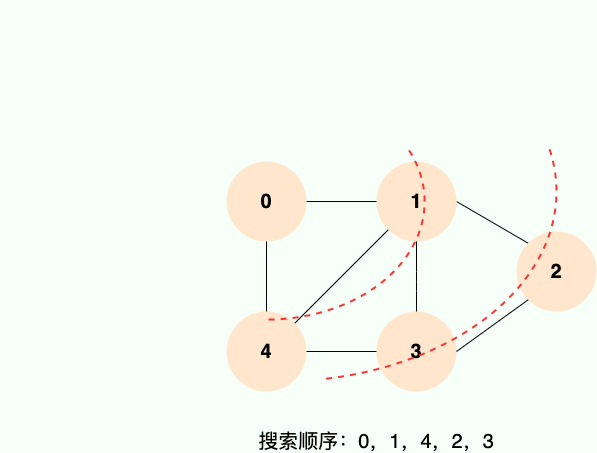
广度优先搜索就像水面上的波纹一样一层一层向外扩展,如下图所示:
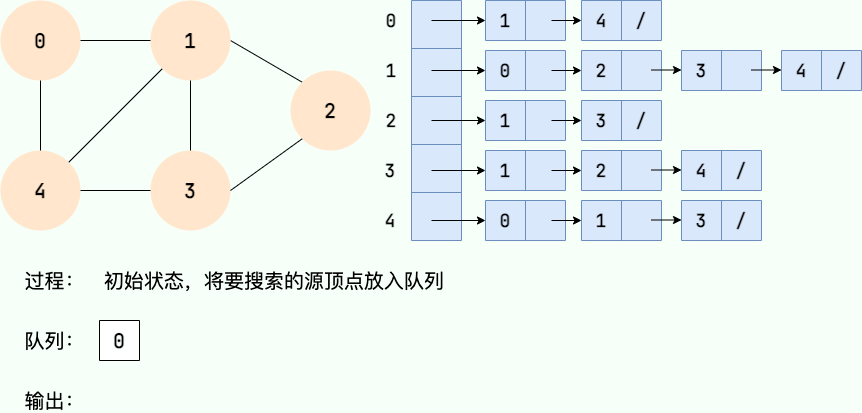
广度优先搜索的具体实现方式用到了之前所学过的线性数据结构——队列 。具体过程如下图所示:
第 1 步:
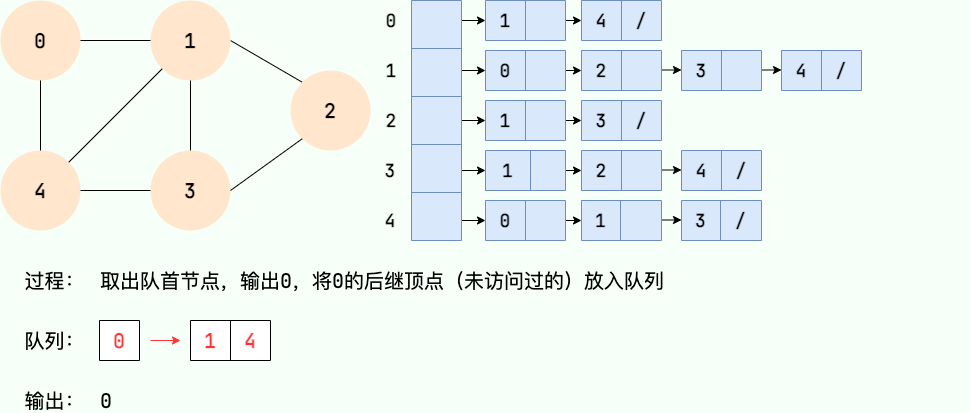
第 2 步:
第 3 步:
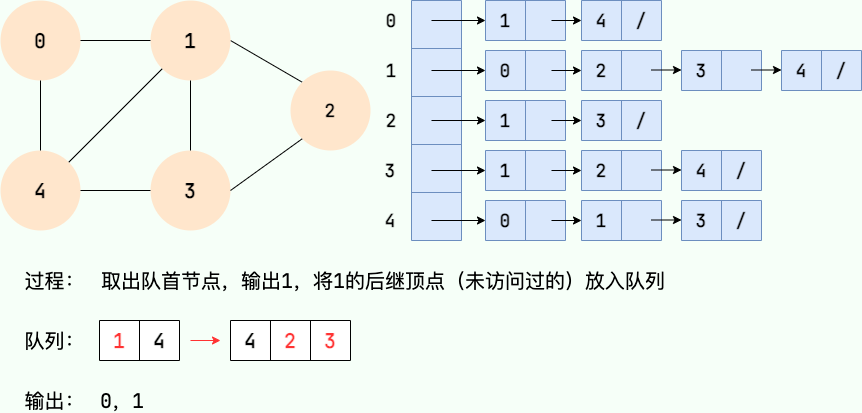
第 4 步:
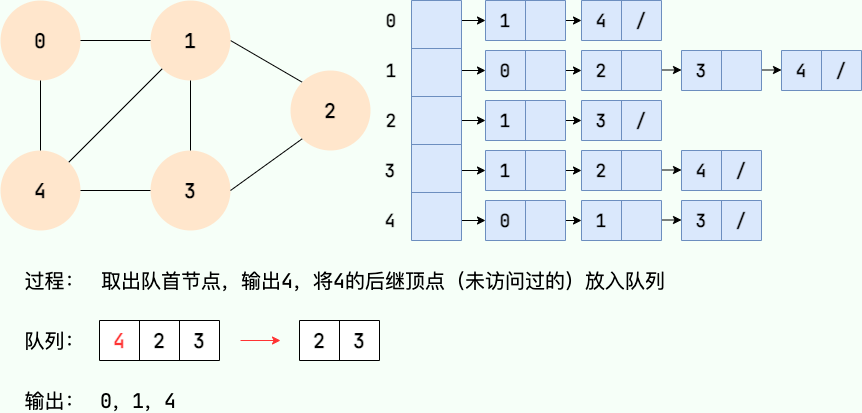
第 5 步:
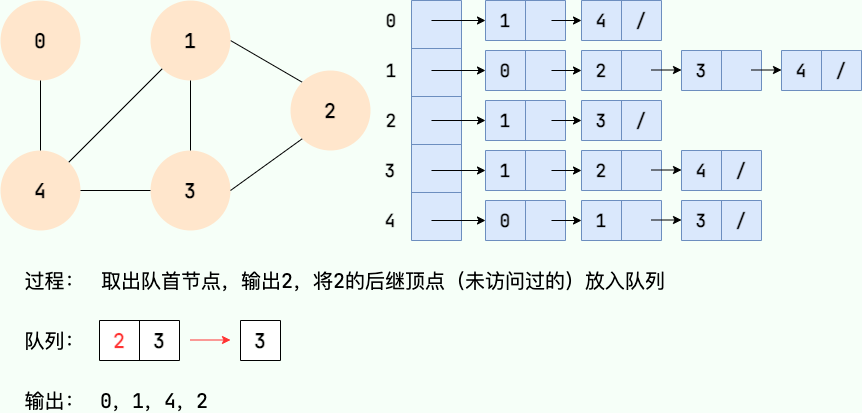
第 6 步:
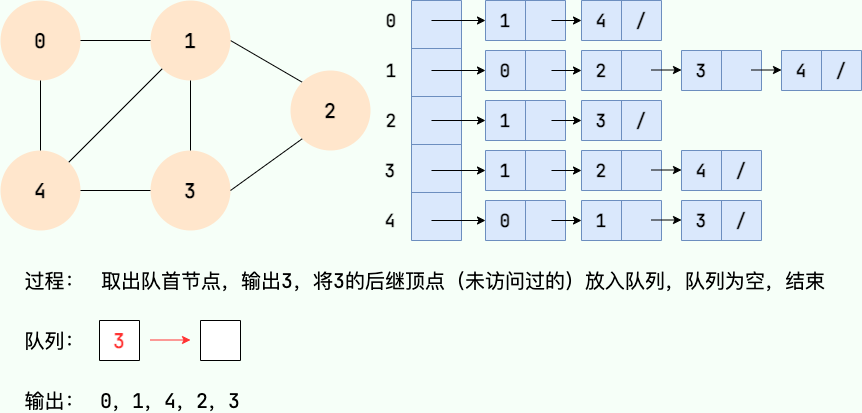
深度优先搜索
深度优先搜索就是“一条路走到黑”,从源顶点开始,一直走到没有后继节点,才回溯到上一顶点,然后继续“一条路走到黑”,如下图所示:
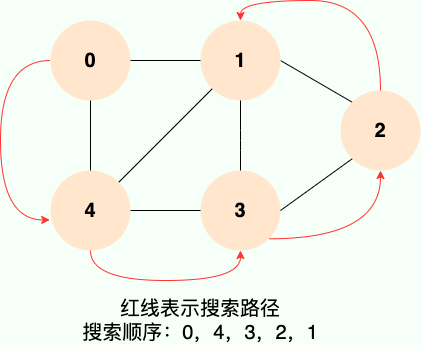
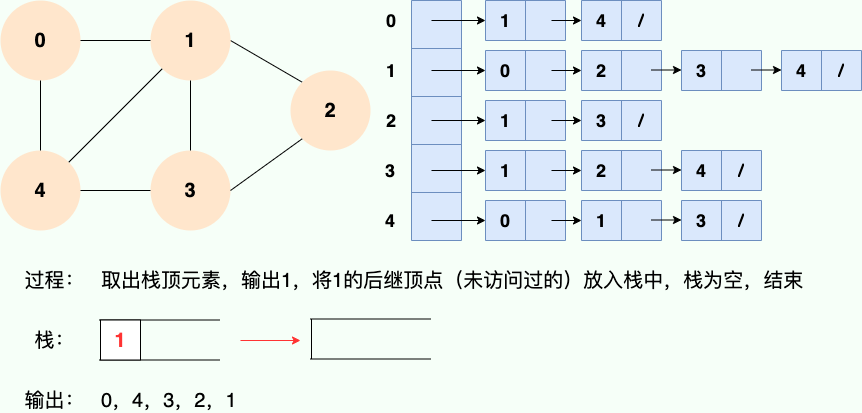
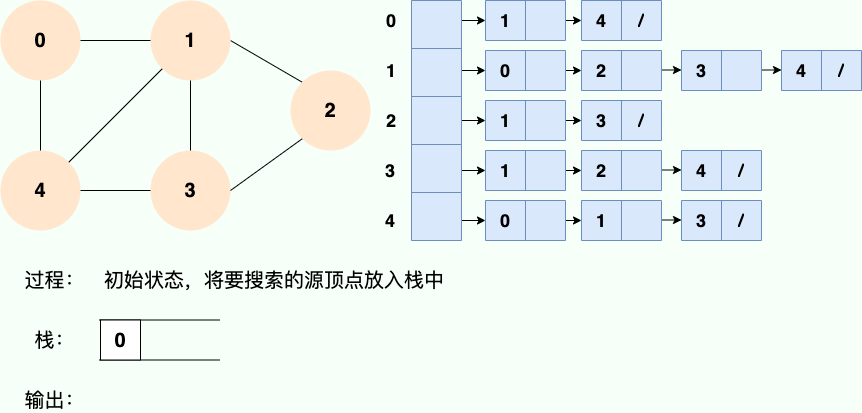
和广度优先搜索类似,深度优先搜索的具体实现用到了另一种线性数据结构——栈 。具体过程如下图所示:
第 1 步:
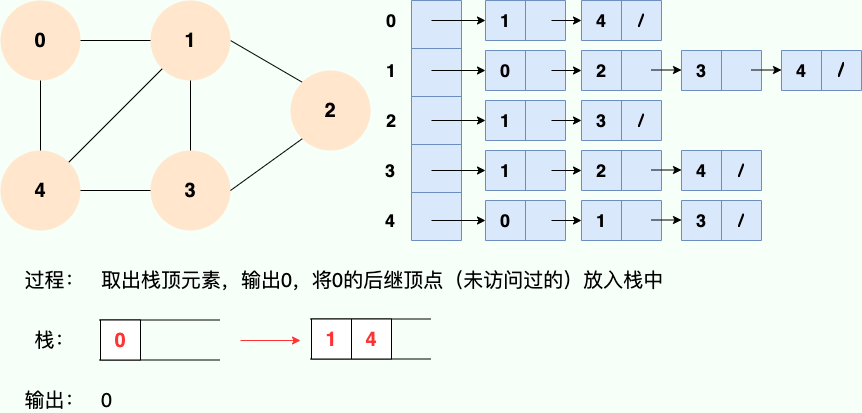
第 2 步:
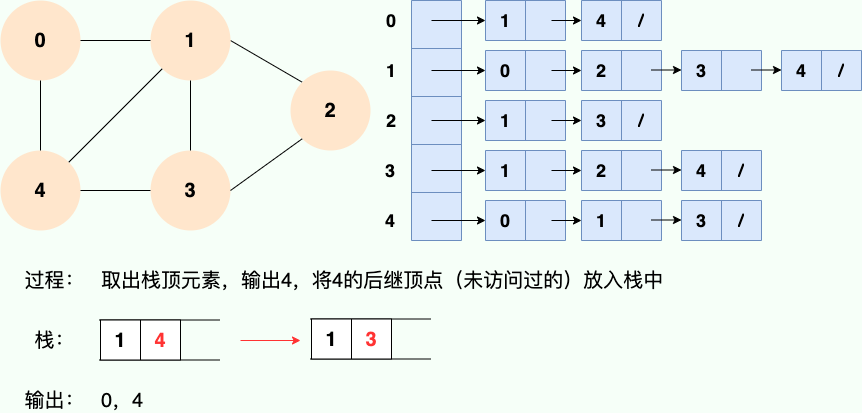
第 3 步:
第 4 步:
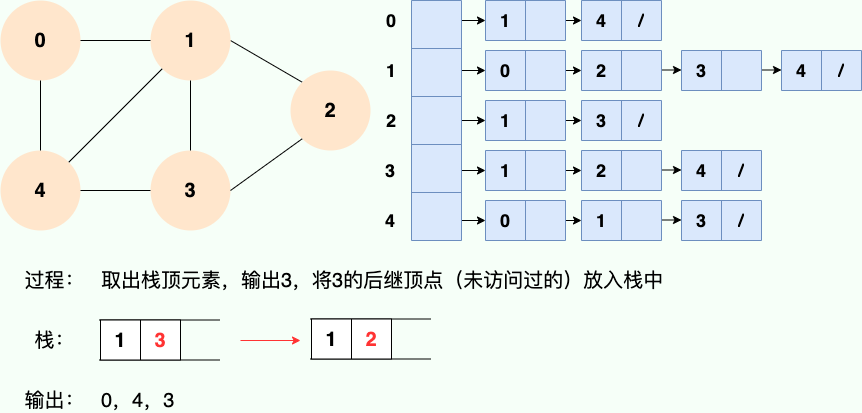
第 5 步:

第 6 步: